Глава вторая

ЭЛЕМЕНТЫ ДИНАМИКИ ДВИЖЕНИЯ ВО ВРЕМЕНИ

2.1. Закон сохранения количества движения во времени

Все мы понимаем, что непрерывно движемся во времени из прошлого в будущее вместе с окружающими нас предметами. Тем не менее до сих пор не существует целостной теории движения во времени. Рождение таковой задерживало, как ни странно, изобретение часов. Ибо с появлением механических часов, стрелки которых "идут" мелкими шагами, люди стали говорить не о движении времени, а о "ходе времени", как еще раньше, с изобретением водяных и песочных часов - клепсидр, начали говорить о "течении времени", наблюдая за течением воды или песка в этих часах.
Поэтому, когда в 1905 г. А. Эйнштейн предложил СТО, он заявил, что из нее следует, что ход времени зависит от скорости движения в пространстве. Про движение во времени даже речи не было. Эйнштейн изучал закономерности движения в пространстве, а затем и само пространство. Исходя из только-только открытого тогда факта, что в природе не существует скоростей, больших скорости света в вакууме С, он говорил о "ходе времени".
Лишь в 1908 г. Г. Минковский, помогавший Эйнштейну разрабатывать математический аппарат теории относительности, догадался, что пространство и время взаимосвязаны, и объединил их в единое четырехмерное пространство-время, в котором движутся все тела.
Однако четырехскорость Минковского, о которой мы говорили в разделе 1.2, была далеко не лучшим изобретением СТО - ее недостатки слишком бросались в глаза. Поэтому после смерти Минковского в 1909 г. этим понятием пользовались редко. Потому-то все до сих пор говорят о "ходе времени", а не о движении во времени, упуская из-за этого из вида динамические параметры движения тел во времени.
Это все равно, что говорить "бег дороги" вместо "бег автомобиля по дороге". Некоторые скажут, что не видят особой разницы между этими двумя выражениями, поскольку движение - понятие относительное. Но все же на повороте заносит авто-обиль, а не дорогу. Поэтому для безопасного движения автомобиля учитывают его скорость и массу (произведение этих величин называют импульсом), а не массу дороги.
Мы уже говорили, что Е. Л. Фейнберг в [7] выражал беспокойство о том, что адиционный кинематический подход к СТО делает ее формальной наукой. Он указал, что для улучшения понимания предмета надо бы исходить из динамических хактеристик движения, и сетовал, что этого никто не сделал. Но сделать это, исхо-
13 динамических характеристик движения тел в пространстве, было, по-видимому, невозможно, а рассматривать динамические характеристики мнимого движения во времени никому, увы, и в голову не приходило до появления работы [8].
В ней впервые было показано, что если учесть динамические параметры движения тел во времени, как учитывают аналогичные параметры движения автомобиля по дороге, то в СТО, столь трудной для понимания, все становится очень простым и ясным.
Хотя мнимого движения тел во времени мы не видим, попробуем представить, чти оно в какой-то мере подчиняется законам обычной классической механики, в которой скорость V перемещения тела в пространстве заменим скоростью у движения его во времени. По аналогии с известным уравнением закона сохранения обычного импульса (количества движения) Р = mV в системе центра инерции

(2.1)

составим уравнение для закона сохранения количества движения тела во времени:

(2.2)

Здесь m0 - масса неподвижного в пространстве тела (масса покоя), т - масса того же тела при движении его в пространстве.
Мы воспользовались частным случаем уравнения для закона сохранения импульса (2.1). В нем m1 и V, - это, например, масса и скорость пули, а m2 и V2 - соответственно масса винтовки и скорость отдачи, приобретаемой винтовкой при выстреле. Это же уравнение (2.1) описывает и закон сохранения импульса вагона, свободно катящегося по рельсам под мостом, с которого в вагон насыпают песок. Если до моста масса вагона была та скорость V1, то после моста масса вагона с песком возрастает до m2. При этом импульс вагона Р остается неизменным.
То же самое справедливо и при движении тела во времени. Только теперь не скорость движения является функцией от массы движущегося тела, как было в примере с вагоном, а наоборот: величина массы тела зависит от скорости у движения данного, тела во времени. Это и отражает уравнение (2.2) и получаемая из него простым алгебраическим преобразованием известная в СТО формула для релятивистской массы

(2.3)

Ее вывод в учебниках по СТО особенно сложен. Мы же получили ее почти шутя, учитывая, что у= 1.
Из (2.3) понятно, что масса тела возрастаете увеличением скорости У его движения в пространстве. (Так как . СТО объясняет, что это увеличение массы тела вызывается тем, что в массу превращается кинетическая энергия, сообщаемая телу при его ускорении. А вот из теории движения не только понятна причина возрастания массы, но и объясняется закон, по которому происходит это увеличение массы. Оно обусловлено действием закона сохранения количества движения тела во времени. Это один из важнейших законов природы наряду с хорошо всем известным законом сохранения обычного импульса.
Вооружившись законом сохранения-количества движения во времени, мы теперь можем приступить к реализации мечты Е. Л. Фейнберга о выводе основных уравнений формул СТО исходя из динамических характеристик движения тел. Посмотрим, например, что происходит с размерами тел при их движении в пространстве-времени. Для этого домножим обе части уравнения (2.2) на некоторую длину l0, измеренную вдоль направления движения тела в пространстве. Этим мы превратим данное уравнение в уравнение для закона сохранения момента количества движения тела во времени:

(2.4)

Вектор мнимой скорости l движения тела во времени всегда перпендикулярен вектору действительной скорости ßдвижения его в пространстве, поскольку векторы действительной и мнимой частей вектора J, изображающего комплексное число на комплексной плоскости, всегда ортогональны. Значит и соответствующие им векторы действительного (m ß) и мнимого (mу) импульсов также взаимно перпендикулярны. А длину отрезка l0 мы выбрали вдоль вектора m ß значит, перпендикулярно мнимому вектору ту. Поэтому векторное произведение вектора mу на перпендикулярный ему радиус-вектор l0 есть не что иное, как момент мнимого количества движения во времени относительно начала отрезка l0. Само же уравнение (2.4) выражает закон сохранения момента количества движения тела во времени.
Обозначим произведение l0у в уравнении (2.4) как некую новую длину l, а величину m заменим ее значением m0lу из формулы (2.3). Тогда уравнение (2.4) превратится в тождество, и мы тем самым докажем известную формулу СТО для лоренцева сокращения длин при движении тел:

(2/5)

Как видим, она тоже выводится из закона сохранения количества движения тела во времени. Это один из основных законов физики, вытекающий, как и закон сохранения обычного импульса, из общепризнанного постулата об однородности пространства Вселенной.
Если же мы возьмем отрезок l0 не вдоль, а перпендикулярно направлению щижения тела в пространстве, то векторное произведение l0 на mу будет равно нулю при любых значениях у (как векторное произведение параллельных векторов).
Поэтому в последнем случае l1 = l0 при любых у. То есть размеры тел в направлениях, перпендикулярных направлению их движения в пространстве, остаются неизменными при любых скоростях движения.
Ну а формулу СТО для релятивистского замедления хода времени на движущихся телах

(2.6)

нам и выводить не надо. Она непосредственно вытекает из данного в разделе 1.3 определения безразмерной скорости у.
Разберем теперь, что такое преобразования Лоренца, о которых уже упоминалось выше. Когда вы едете в поезде и находитесь на расстоянии X' от задней стенки последнего вагона, то расстояние от Вас до станции, от которой отъехал поезд, составляет:

(2.7)

Здесь U - скорость поезда, г- время в пути. Такие вычисления в классической механике называют преобразованиями Галилея при переходе от движущейся к неподвижной системе отсчета координат. Много веков считалось, что при переходе от движущейся к неподвижной системе отсчета остаются неизменными длины отрезков и время, а вот скорости движения суммируются геометрически как векторы. Так, скорость Вашего движения по вагону суммируется со скоростью поезда, и относительно столба на обочине дороги Вы движетесь уже с большей скоростью, чем относительно вагона.
В конце XIX века результаты опыта Майкельсона указали, что свет от фар едущего паровоза летит вперед относительно паровоза с такой же скоростью, с какой он летит, в тот же момент и относительно столба на обочине дороги. Это открытие потрясло физиков. Начались поиски таких преобразований координат, которые оставляли бы скорость света С неизменной при переходе от движущейся к неподвижной системе отсчета. Они были найдены в 1904 г. X. Лоренцем.
Поскольку мы уже знаем, как зависят длина тела и ход времени на нем от скорости движения тела в пространстве, то для нас уже не составит особого труда вывести: формулы преобразований Лоренца.
Для едущего в поезде наблюдателя кажется, что это не поезд едет, а окрестным поля и леса движутся относительно него в обратную сторону со скоростью - U. Поэтому расстояния Х до станции (отмеченные верстовыми столбами вдоль дороги) на движущейся относительно него земле подвергаются лоренцевому сокращению по формуле (2.5) и становятся для него равным Х'=Ху, где - скорость движения поезда во времени. Тогда вышеприведенное выражение для преобразования Галилея (2.7) превращается в формулу преобразования Лоренца, для пространственных координа:

(2.8)

А формулу преобразования Лоренца для времени выведем из вышеприведенного выражения (2.6), возведя его в квадрат и разделив обе его части на t. Учтя, что получим:

(2.9)

Здесь - время, измеряемое собственными часами пассажира поезда, а t -время, измеряемое часами на станции. Понятно, что, когда поезд был еще на станции (Х= 0), показания обоих часов совпадали.
Ну и, наконец, выведем формулу сложения скоростей СТО, которая даст ответ на вопрос, почему столь странные результаты получились в опыте Майкельсона и в; опытах Физо. Когда пассажир поезда шагает вперед по ходу поезда со скоростью V' относительно вагона, то расстояние X' пройденное пассажиром в вагоне за собственное время т, измеренное часами в вагоне, составит величину X'= 1/. Подставим это выражение вместо X' в формулы (2.8) и (2.9), а затем разделим (2.8) на (2 9) В результате получим формулу для суммарной скорости движения пассажира относительно земли, по которой едет поезд:

(2.10)

(Эту формулу сложения скоростей за 7 лет до Эйнштейна опубликовал Дж. Лармор.) Из найденной формулы понятно, что, поскольку скорости V' и U не могут превышать величину скорости света С, то суммарная скорость VЕ ни при каких обстоятельствах не превысит скорость света в вакууме С.
Начав этот раздел с разговора о количестве движения во времени, давайте и закончим его разговором об этом мнимом импульсе mу. Домножив обе части уравнения (1.16) на m2с2(m квадрат с квадрат) и вспомнив, что mу = m0у0, получим выражение:

(2.11)

Из него видим, что сложение реального импульса движения тела в пространстве Р = mV и мнимого импульса движения того же тела во времени mСу = m0Су0 осуществляется по правилу сложения взаимно перпендикулярных векторов. Это еще раз напоминает нам, что указанные импульсы, как и соответствующие им скорости движения тела в пространстве и во времени, всегда взаимно ортогональны как реальная и мнимая части комплексного числа.
А домножив почленно обе части уравнения (2.11) на С2(c квадрат), получим известное в СТО уравнение:

(2.12)

связывающее полную энергию тела Еn = mС2(c квадрат) с его массой покоя ту и импульсом Р. Только здесь эти формулы несут гораздо больше информации, чем в СТО.
Эти формулы скоро понадобятся нам. А отсылать читателя за ними к учебникам по СТО мы постеснялись, ибо тогда ему пришлось бы "перелопатить" десятки страниц, и неизвестно еще, с каким результатом. Наш же вывод с помощью теории движения во времени занял всего несколько страниц. Надеемся, что преподаватели физики с Удовольствием возьмут его на вооружение. Это позволит им и их слушателям экономить немало времени даже без "машины времени", к изобретению которой (чем черт не шутит!) может привести дальнейшая разработка теории движения во времени.

2.3. Что такое энергия покоя тела?

Для понимания дальнейшего в теории движения и вихревой энергетике нэп понадобится одна очень важная формула. А именно - знаменитая формуя Эйнштейна, связывающая массу с энергией Е = mС2(c квадрат). До Эйнштейна в классическо! механике полагали, что кинетическая энергия движения тела в пространств) определяется формулой

(2.13)

в которой m0 - масса покоя тела, движущегося со скоростью V. Изучая фотоэффект и давление света, экспериментально открытое П. Лебедевым, А. Эйнштейн пришел к выводу, что безмассовые фотоны света несут с собой не только энергию определяемую формулой Планка но и импульс Р = Е/С. Ну а поскольку
импульс Р - это произведение массы тела на его скорость, а скорость фотонов свет: С, то в данном случае Р = mС. Отсюда следовало для фотонов:

(2.14)

То есть безмассовые фотоны при движении как бы приобретали эффективную массу тем большую, чем больше энергия фотона. Эйнштейн выдвину, предположение, что эта формула справедлива не только для фотонов, но и для любы тел. При этом масса т в данной формуле - это полная (релятивистская) масс движущегося тела, определяемая выражением (2.3). Из него следует, что покоящемуся в пространстве телу (имеющему массу покоя m0) соответствует энергия

(1.15)

Эйнштейн назвал ее "энергией покоя" тела, или "внутренней энергией" тела Почему внутренней? - Потому что в начале XX века люди представляли себе элементарные частицы вещества чем-то вроде сильно сжатых пружин, удерживаемых о распрямления какими-то огромными силами неизвестной природы. Энергию эти сжатых "пружин" (или прижатых друг к другу отталкивающихся электрических зарядов - составных элементов частицы) и назвали внутренней энергией вещества.
Расчеты по формуле (2.15) показывали, что в каждом грамме любого веществ содержится столько внутренней энергии, что если бы ее высвободить и превратить электроэнергию, то хватило бы на год отоплять и освещать целый город. Но в начал XX века никто не знал, как высвободить эту энергию. Лишь последующее развитии ядерной физики, физики элементарных частиц и ядерной энергетики с высоко точностью подтвердило догадку Эйнштейна и правильность формулы (2.15).
Но никто до сих пор не мог объяснить, что это за "энергия покоя" и откуда он берется. Да и строгого вывода формулы (2.15) не существовало. Сам Эйнштейн при ее выводе в [16] использовал методы приближенного исчисления, дающие заведомо не очень точные результаты. А последователи гения, угадавшего эту формулу, по примеру В. Паули пытались найти точный вывод ее с помощью интегрального исчисления. В некоторых справочниках (например, в [17]) до сих пор фигурирую этот "вывод":

(2.16)

За математической безукоризненностью этих формул составители справочников проглядели один физический "прокол". А именно, под знаком интеграла мы видим выражение. Дифференциалы в нем означают пределы бесконечно малых величин ∆Р и ∆l при ∆t, стремящемся к нулю. Но соотношение неопределенностей квантовой механики, открытое В. Гейзенбергом пять лет спустя после публик В Паули вышеприведенного "вывода" формулы Эйнштейна, гласит, что произвел не может быть меньше величины постоянной Планка h. Значит, в (2.16] знаком интеграла . И при это выражение стремится к бесконечности вместо ожидаемой бесконечно малой величины С2(c квадрат)dm. Так квант механика зачеркнула труд разработчиков теории относительности, пользовавшихся классической механикой с ее бесконечно малыми величинами. Остается то удивляться составителям современных справочников.
Но ценность формулы Эйнштейна от этого не уменьшается, она блестяще подтверждается работой атомных электростанций, в которых высвобождает используется часть энергии покоя урана.
Современный французский критик теории относительности Л. Бриллюэн отмечал, что формулу Эйнштейна "невозможно вывести ни из о, существующей в настоящее время теории или модели", как и формулу М. Планка . Он писал, что эти угаданные двумя гениями формулы - "не результат исходный пункт нашего мышления", что смысл "троицы", энергия = масса = час составляющей итог всех законов физики, все еще находится в глубокой тайне".
В книге [8] указан еще один возможный ответ на вопрос о том, что такое энергия покоя тела. Из закона всемирного тяготения Ньютона вытекает, что всякое тело со; вокруг себя гравитационное поле (поле тяготения), каждая точка которого характеризуется потенциалом

(2.17)

Здесь С- постоянная тяготения, т - масса тела, г- расстояние от центра м; тела до рассматриваемой точки. Гравитационный потенциал показывает, какой энергией гравитационного взаимодействия с данным телом будет обладать в данной точке поля другое тело, имеющее массу m1.
Энергтя гравитационного взаимодействия

(2.18)

обусловлена силами притяжения тел друг к другу. Это энергия связи тел, и ее при тать отрицательной. Например, энергия гравитационной связи с Землей яблока, лежащего на ее поверхности и имеющего массу кг, составляет -6-106(десять в шестой степени). Чтобы поднять яблоко и забросить его в дальний космос, где притяжение Земли уже изчезающе мало, надо совершить положительную работу 6-106(десять в шестой степени) Дж. Сумма этой положительной энергии и найденной выше отрицательной энергии связи и даст почти нулевую энергию связи яблока с Землей в дальнем космосе.
В этом примере мы учли притяжение яблока только к Земле. Но на него действ еще и поля тяготения от Луны, Солнца и других бесчисленных тел Вселенной Попробуем вычислить суммарный гравитационный потенциал, создаваемый всеми ими, а затем и суммарную энергию гравитационной связи нашего яблока со всеми телами Вселенной. На первый взгляд эта задача может показаться немыслимой, ибо Вселенная безгранична, а расстояния до небесных тел так велики...
Но по современным представлениям Вселенная имеет конечный объем. определяется радиусом кривизны ее пространства (или, для краткости, про радиусом Вселенной). В этом объеме довольно равномерно распределены галактики, составляющие массу Вселенной г. Величины хоть и не очень точно, но уже вычислены астрофизиками по результатам многочисленных наблюдений. А согласно космологическому принципу Эйнштейна все точки Вселенной равноценны. Поэтому любую из них можно рассматривать находящуюся на расстоянии R0 от "центра массы" Вселенной. Тогда гравитационный потенциал, создаваемый всей массой Вселенной в точке, где находится наше яблоко (как и в любой другой точке), будет как на поверхности шара с радиусом и массой Вселенной и составит величину

(2.19)

Подставив сюда числовые значения, увидим, что 0 приблизительно равен квадрату скорости света -С2(с квадрат), но со знаком минус. (Гравитационный потенциал имеет размерность квадрата скорости.)
Вычислим теперь энергию гравитационной связи тела со всеми остальные телами Вселенной как произведение массы этого тела на гравитационный потенциал Вселенной:

(2.20)

Итак, мы неожиданно получили формулу, очень похожую на знаменитую формулу Эйнштейна для энергии покоя тела! Но формула (2.20) определяет потенциальную энергию тела в гравитационном поле Вселенной. Так это и есть "энергия покоя" тела ?
Видим, что с этой точки зрения величина -С2(с квадрат) в формуле Эйнштейна - это просто квадрат скорости света, а гравитационный потенциал Вселенной.
Приблизительное, а не строгое равенство мы получили потому, что не очень то знаем величины. Но строгое равенство не доказано ни в одном известном выводе формулы Эйнштейна. Не исключено, что за неточностью этого равенства кроется будущая фундаментальная теория, развивающая далее теорию относительности. Ведь и казавшаяся в прошлом столь точной механика Ньютона тоже, как оказалось, давала только приблизительные значения вычисляемых величин. За этой неточностью скрывалась релятивистская механика, без которой невозможно решать такие, например, задачи, как движение частиц в ускорителях, где скорости приближаются к скорости света С.
Полученная формула (2.20) отличается от эйнштейновской еще и знаком минус потому что энергия гравитационной связи считается отрицательной. На это мои было бы сказать, что знак - дело условное, и напомнить, что на самом деле отрицательных энергий не бывает, как и отрицательных масс. Что отрицательная
энергия связи в системе из нескольких тел, например в атоме, - это всего лиш недостача положительной массы-энергии до какой-то большей величины. А в целом сумма всех энергий системы остается положительной величиной. Но в следующих разделах книги мы найдем более интересный ответ на этот вопрос об отрицательных
энергиях.
А здесь еще раз отметим, что как висящее на дереве яблоко обладает потенциальной энергией, которая высвобождается при падении яблока на земли так и все "висящие" в пространстве Вселенной тела тоже обладают такого же рода потенциальной энергией . Но только они не могут "упасть" к "центру Вселенной", как не падает на планету ее спутник.

2.4. "Импульс покоя" тела и особые скорости движения

В разделе 1.2. предыдущей главы мы критиковали определение (1.1 "четырехскорости" Минковского, в котором действительная часть при 2 принимала значения, большие скорости света С. Это получилось потому, что величин расстояний l и времени при этом брали из разных систем отсчета, что некорректно
Но именно так экипажам космических межзвездных кораблей в будущем удобн( всего будет выражать и измерять "собственную скорость" корабля:

(2.21)

Ведь расстояния l до той или иной звезды указаны в атласах по земным мерка? а время полета корабля г экипажу удобнее измерять по своим собственным часам "Собственная скорость" может оказаться и больше скорости света С, хотя для земного наблюдателя скорости V0 будет соответствовать скорость V = V0у, всегда меньше скорости света С.
А вычисляя импульс своего корабля, его экипаж будет просто умножать масса покоя корабля m0 на "собственную скорость":

(2.22)

И в самом деле, не пересчитывать же каждый раз массу корабля по релятивистской формуле (2.3) зависимости массы от скорости! Для космонавта масса его корабля как и масса его собственного тела, не зависит от скорости корабля, а всего представляется ему равной массе покоя m0, которая в СТО считается инварианта
при преобразованиях Лоренца, так же, как считается инвариантным собственное время.
Получаемая по (2.22) величина импульса соответствует релятивистскому импульсу корабля, вычисляемому земным наблюдателем по формуле Р = mV, в которой m = m0/y релятивистская масса корабля.
По аналогии с существующим в СТО выражением "энергия покоя" тела назовем величину "

(2.23)

импульсом покоя" тела. Он, конечно же, равен рассмотренному в разделе 2.1 количеству движения во времени (2.2) тела, покоящегося в пространстве и инвариант при преобразованиях Лоренца.
В формулах (2.21) и (2.22) появился любопытный сомножитель - отношение ß/y на который обращалось внимание еще в книге [8]. Это отношение озна безразмерную собственную скорость тела

(2.24)

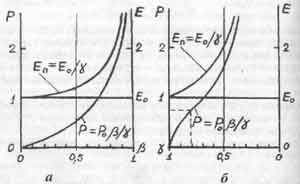
В книге [8] была обнаружена точка перегиба на графике зависимости Ф от y. А ведь графики давно известных в СТО зависимостей релятивистского импульса Р и полной (релятивистской) энергии тела от безразмерной скорости ß движения данного тела в пространстве (см. рис. 2.1 а) не имеют особых точек. Последнее вполне соответствовало эйнштейновскому утверждению о равноправии всех скоростей движения. Эйнштейн многократно подчеркивал, что в природе нет выделенных (особых) скоростей движения, ибо это вытекало из его постулатов. И вот на графике функции Ф (у), а также на графиках V0(у) и Р(у), которые выражаются одной и той же кривой, построенной на рисунке 2.1 б, мы видим точку перегиба при3(ей соответствует скорость движения в пространстве . В [8] обнаружены и
перегиба на графиках еще двух функций (при и при у ~ 0.933)
наибольшую важность для нас имеет, конечно же, приведенная здесь кривая зависимости импульса тела Р от скорости у движения этого тела во времени.
Эйнштейновское утверждение о равноправии всех скоростей предполагало отсутствие особых точек на графиках зависимостей энергии и импульса тела от его скорости. Но никому не приходило в голову строить графики зависимостей величин от какого-то "фактора Лоренца", как называли величину 2(бетта в квадрате)
догадываясь, что она означает скорость движения тела во времени.

Рис. 2.1

Отмеченные выше скорости, соответствующие точкам перегиба графиков, можно назвать особыми скоростями движения. Следует согласиться, что скорость с вакууме С - тоже особая скорость, можно сказать, самая особая, мировая коне Следующая за ней по важности - особая скорость , которая в [8] названа "первой космической скоростью Вселенной" в предложении, что с такой скор движутся наиболее отдаленные от нас галактики, и что именно с такой скор движется относительно "центра масс Вселенной" каждое ее тело. При этой скорости ß = у и потому достигается равнораспределение энергий движения в пространстве и во времени и наблюдается ряд экстремумов на графиках, строившихся в [8].
Отмеченные выше скорости, соответствующие точкам перегиба графиков, можно назвать особыми скоростями движения. Следует согласиться, что скорость с вакууме С - тоже особая скорость, можно сказать, самая особая, мировая коне Следующая за ней по важности - особая скорость , которая в [8] названа "первой космической скоростью Вселенной" в предложении, что с такой скор движутся наиболее отдаленные от нас галактики, и что именно с такой скор движется относительно "центра масс Вселенной" каждое ее тело. При этой скорости ß = у и потому достигается равнораспределение энергий движения в пространстве и во времени и наблюдается ряд экстремумов на графиках, строившихся в [8].
Называя указанные скорости движений особыми, мы, казалось бы, замахиваемся на то, что еще недавно считалось святая святых современной физики - постулаты Эйнштейна. Но ведь найденные точки перегибов и экстремумов существуют! От этого факта уже не отмахнуться, как не отмахнуться и от наличия во Вселенной выдел (абсолютной) системы отсчета, связанной с реликтовым излучением. Остается только выяснить, в каких процессах проявляются эти особые скорости.
Кстати, с особой скоростью мы имеем дело повседневно: т минимальная скорость распространения света (электромагнитных волн) в Случайно ли? Ведь вода хранит в себе столько тайн и обладает столь удивительными аномальными свойствами, отличающими ее от других веществ. А совпадения природе редко бывают лучайными.

2.5. Что такое силы инерции?

Они появляются при ускорении тел и противодействуют внешним с вызывающим ускорение тела. По своей величине сила инерции всегда точно ускоряющей силе и всегда направлена противоположно ей. То есть

(2.25)

где - вектор ускорения, возникающего под действием внешней силы .
Эта формула написана на основании третьего закона Ньютона: действие противодействию. Но в справочниках Вы вряд ли найдете ее. Объясним почему. В данном случае сила инерции противодействует внешней силе F, вызывающей ускорение тела в пространстве, описываемое вторым законом Ньютона:

(2.26)

который прекрасно вписался в современную физику. Но вот отчего возн противодействие, как появляются эти силы противодействия, то есть силы ине никто до наших дней ответить не смог. Другими словами, не смогли вы аналитически формулу (2.25), исходя из формулы (2.26) - никак не получала минуса.
Со времен Э. Маха бытует мнение, что силы инерции обусловлены гравитационным взаимодействием тела со всеми остальными телами Вселенной. Но почему тогда проявляются мгновенно? Ведь до остальных тел Вселенной так далеко, а теория относительности утверждает, что взаимодействие не может передаваться мгновенно! Этот вопрос тоже остается без ответа и мучает физиков. Силы инерции - одна из самых больших загадок физики. Не сумев объяснить их, физики в последние десятилетия начали даже изгонять упоминания об этих силах со страниц учебнике Так, например, бытовавшее ранее выражение "центробежные силы" (они являют одним из проявлений сил инерции) напрочь исчезло из литературы. Вместо это теперь говорят о противодействующих центробежным центростремительных силе описываемых формулой (2.26), забывая, что у всякой силы всегда имеется противодействующая ей.
В [9] было сделано предположение, что гравитоны являются тахионами, а любые гравитационные взаимодействия могут распространяться почти мгновенно на любые расстояния. Это возвращает нас на позиции принципа дальнодействия сил гравитации, выдвинутого И. Ньютоном. Кроме того, это объясняет мгновенное проявления сил инерции как результата гравитационного взаимодействия тела ? всеми остальными телами Вселенной.
В [8] с помощью теории движения во времени выведена формула (2.25) исходя из (2.26), т.е. сделано то, что до сих пор не удавалось поколениям механиков. Для это было вычислено ускорение движения тела во времени как производная по dt от y.

(2.27)

Это ускорение имеет размерность, обратную размерности времени, поскольку скорость движения во времени ?- величина безразмерная. Но самое интересное это то, что ускорение движения во времени у имеет знак, противоположный знаку ускорения движения того же тела в пространстве V·. То есть последнему соответствует замедление движения тела во времени.
Но, как следует из формулы (2.27), ускорение движения во времени зависит еще и от параметра ß/y, названного нами безразмерной собственной скоростью движения тела. Этот параметр возрастает с ростом скорости V движения тела в пространств. Следовательно, ускорение движения тела во времени должно возрастать по абсолютной величине с ростом скорости движения этого тела в пространстве. Последнее обстоятельство совершенно непривычно для людей, привыкших иметь дело с классической механикой.
Если выражение (2.27) домножить на массу тела m, то получается выражение для силы, аналогичное формуле (2.25):

(2.28)

(На скорость света С умножили для обеспечения привычной размерности сил как ранее мы иногда умножали у на С.)
Полученное выражение (2.28), имея требуемый знак минуса, удивительно похоже на выражение (2.25) для сил инерции. Только малопонятный параметр ß/y мешает полному совпадению формул. Но если в формуле (2.28) величину ускорения V не связывать с величиной параметра ?/?, то есть считать независимой от него (или считать отношениеß/y постоянно равным единице), тогда формула (2.28) превратится в формулу (2.25) для сил инерции!
Но разве возможно, чтобы тело ускорялось, а отношение ß/y оставалось неизменным? Разве бывает так, что тело ускоряется, а абсолютная величина скорости его движения не изменяется? Оказывается, бывает. Так, центростремительное ускорение, перпендикулярное тангенциальной скорости Vr движения тела по круговой траектории, не изменяет абсолютную величину этой скорости.
В [8] сделано предположение, что фигурирующие в выражении (2.28) величины ? и ? относятся не к локальному движению тела под действием ускоряющих его локальных внешних сил, а к вселенскому движению вещества в гравитационного замкнутой Вселенной вокруг ее "центра масс", аналогичному движению спутника Земли по круговой орбите. Только если первая космическая скорость у поверхности Земли составляет 7,9-103(10 в третей степени) м/сек, то "первая космическая скорость" для всей Вселенной, имеющей массу ~1055 г и радиус ~1028 см, должна составлять C/V2 . Именно при такой скорости тела ß/y. Это та самая особая скорость, на которую мы уже обратили внимание выше.
Остается только допустить, что локальные ускорения тел под действием тех или иных локальных сил не изменяют абсолютной величины скорости "орбитального" движения этих тел относительно "центра масс" Вселенной, а только изменяют ее направление. Но в разделе 1.3 мы уже видели, что изменение скорости движения тела в пространстве не изменяет абсолютной величины |C| комплексной скорости J движения тел. Следовательно, при переходе к космологическим масштабам надо говорить уже не о движении в пространстве, а о движении в пространстве-времени, как на это давно указывает теория относительности.
Таким образом, можно полагать, что в формуле (2.28) отношением ß/y характеризует не локальные движения тел, а движения вещества Вселенной в целом по круговой траектории. И можно говорить, что силы инерции действительно зависят от движения вещества Вселенной в целом, но возникают как силы ускорения движения тела во времени.

Выводы к главе

1. Подход с позиций динамики к пониманию движения во времени тела с массой m требует выполнения закона сохранения количества движения тела во времени my = m0y0, в котором m0 - масса покоя тела. Из него непосредственно следует формула для релятивистской массы m = m0/y.
2. Вывод остальных основных формул специальной теории относительности в теории движения столь же прост, нагляден и понятен.
З. Энергия покоя тела, которую называют еще внутренней энергией тела, выражаемая формулой Эйнштейна E0 = m0C2(с квадрат), численно совпадает с энергией гравитационной связи данного тела со всеми остальными телами Вселенной. При этом квадрат скорости света С2(с квадрат) равен гравитационному потенциалу Вселенной, взятому с противоположным знаком.
4. График зависимости импульса тела от скорости движения его во времени у имеет точку перегиба при , которой соответствует скорость движения в пространстве . Скорость - тоже особая скорость движения. При ней
5. Силы инерции - это силы ускорения движения тела во времени при замедлении его движения в пространстве. С другой сторон, силы инеоции - это силы взаимодействия тела со всеми телами Вселенной. Мнгновенность проявления сил инерции объясняется мнгновенностью распростронения во Вселенной переносчиков этих сил - гравитонов, являющихся разновидностью тахионов.

Содержание

Далее

Наш сайт является помещением библиотеки. На основании Федерального закона Российской федерации "Об авторском и смежных правах" (в ред. Федеральных законов от 19.07.1995 N 110-ФЗ, от 20.07.2004 N 72-ФЗ) копирование, сохранение на жестком диске или иной способ сохранения произведений размещенных на данной библиотеке категорически запрешен. Все материалы представлены исключительно в ознакомительных целях.

Copyright © UniversalInternetLibrary.ru