Ю.С. Потапов - КРИТИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ И ЭЛЕМЕНТЫ КИНЕМАТИКИ ТЕОРИИ ДВИЖЕНИЯ

Глава первая
КРИТИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ И ЭЛЕМЕНТЫ КИНЕМАТИКИ ТЕОРИИ ДВИЖЕНИЯ

1.1. Необходимость модернизации теории относительности

До настоящего времени существовала созданная гением Галилея, Ньютона, Лейбница, Лагранжа, Гюйгенса и других классическая механика с ее динамикой и кинематикой, а также созданная в начале XX века трудами Эйнштейна и его современников (Лоренца, Пуанкаре, Минковского и др.) релятивистская механика с ее представлением о четырехмерном пространстве-времени, в котором осуществляется движение тел.
Релятивистская механика, используемая в основном для расчетов движения элементарных частиц со скоростями, сравнимыми со скоростью света, имела дело только с досветовыми скоростями, поскольку специальная теория относительности (СТО), предложенная А. Эйнштейном в 1905 г. [1], постулировала, что в природе не существует скоростей движения больших, чем скорость света в вакууме С = 2,99792458 o 108 м/с (второй постулат Эйнштейна).
В 60-е годы родилась идея тахионов - гипотетических частиц, движущихся со сверхсветовыми скоростями. Но для описания движения этих частиц разработчики теории тахионов использовали всё ту же релятивистскую механику, хотя она в данном случае далеко не всегда способна была дать требуемые и понятные результаты.
СТО имела дело преимущественно с прямолинейными и равномерными движениями, а при попытках решения задач, связанных с криволинейным или вращательным движением, пасовала и отсылала к общей теории относительности (ОТО), математический аппарат которой оказался слишком сложным и недоступным большинству инженеров. Да и перечень задач, успешно решенных ОТО, остается весьма ограниченным.
В результате теория относительности, называвшаяся многими в середине XX века красивейшей и величайшей теорией всех времен, до сих пор так и не принесла людям ожидаемых от нее грандиозных результатов. Хотя, конечно, создание кинескопа (электронно-лучевой трубки) телевизора, ускорителей элементарных частиц и ядерной энергетики, бывшее невозможным без теории относительности, - это бесспорно важные достижения, но ожидалось нечто большее. Вопреки ожиданиям, теория относительности, "забуксовав" еще в начале 20-х годов, с тех пор фактически так и не продвинулась вперед. Ее сторонники объясняли это законченностью и совершенством теории и создавали культ личности Эйнштейна. Критиковать его теорию считалось недостойным для настоящего ученого*(Журнал "Молодая гвардия" в № 8 от 1995 г. на стр. 70 писал: "В 1964 г. Президиум АН СССР издает открытое постановление, запрещающее всем научным советам и журналам, научным кафедрам принимать, рассматривать, обсуждать и публиковать работы, критикующие теорию Эйнштейна").
Но критики теории относительности давно подметили в ней ряд внутренних противоречий и недоработок. Они обсуждаются, например, в книгах В. А. Ацюковского [2, 3], братьев Брусиных [4], известного французского ученого Л. Бриллюэна [5]. В предисловии к русскому изданию 1972 г. книги Л. Бриллюэна академик АН УССР А. 3. Петров незадолго до своей кончины писал: "Что касается ОТО, то, вопреки довольно широко распространенному мнению, могучее сооружение этой теории покоится на столь шатком экспериментальном фундаменте, что ее можно было бы на-звать колоссом на глиняных ногах... Если, например, историческое развитие квантовой механики доказывает постепенное ее совершенствование, "взросление", все большее повышение ее точности благодаря накоплению экспериментального материала и включению его в теорию, то ОТО до сих пор щеголяет в коротких штанишках "вун-деркинда", которому все дозволено и даже - освобождение от экспериментальной проверки. Для истинного физика такое положение нетерпимо".
А вот в отношении СТО Петров там же отзывается только похвально, хотя СТО тоже полна парадоксов, а значит, внутренних противоречий. Наиболее известен из них "парадокс часов", или "парадокс близнецов", о котором написаны тысячи страниц.
Но в 1972 г. уже семь лет как было открыто реликтовое излучение, которое в 1979 г. позволило измерить абсолютную скорость движения Земли в космическом пространстве [6] и тем самым пошатнуть веру многих в незыблемость постулатов Эйнштейна, провозглашающих, что в природе не существует абсолютной (выделенной) системы отсчета координат и абсолютных скоростей движения, что они только относительны. Появилось множество критиков и ниспровергателей Эйнштейна (большинство из которых - люди недостаточно компетентные и недостаточно самокритичные), называющих себя "нерелятивистами" и стремящихся любыми средствами опорочить и "отменить" теорию относительности. Но никто из них не сумел предложить взамен нее что-либо более простое, более общее, менее противоречивое и, наконец, более понятное.
В этой ситуации требовалось, с одной стороны, отстоять от необоснованных наскоков те моменты теории относительности, которые подтверждаются экспериментами и не противоречат ни логике, ни математике, а с другой стороны, выявить и отбросить все то ошибочное, что существовало в теории относительности, делало ее непонятной и противоречивой и сдерживало ее развитие.
Некоторые сторонники теории относительности тоже понимали необходимость перемен. Так, например, известный российский специалист по теории относительности Е. Л. Фейнберг в [7] выражал беспокойство о том, что традиционный кинематический подход к СТО делает ее формальной наукой, занимавшейся математическими манипуляциями с физическими символами. Он указывал, что для улучшения понимания предмета надо бы исходить из динамических характеристик движения, и сетовал, что никто до сих пор этого не сделал.
В книгах [8] и [9] как раз и сделана попытка такого подхода для построения теории движения взамен СТО. Но прежде чем перейти к изложению основных положений теории движения, разберемся в некоторых ошибках и упущениях теории относительности.

1.2. Основные ошибки и упущения СТО

В теории относительности огромную роль играет представление о четырехмерном пространстве-времени и об интервале как расстоянии между точками в нем. В доэйнштейновские времена полагали, что пространство Вселенной трехмерно и описывается эвклидовой геометрией с декартовыми осями координат х, у, г. Но когда описывают движение тела, например, когда чертят график движения поезда, то вдоль одной оси координат на листе бумаги откладывают расстояния, а вдоль другой - время t. Ось времени - четвертая ось координат - еще с догалилеевских времен неявно присутствовала в описаниях движения тел, только люди не осознавали этого.
Первым осознал Г.Минковский, помогавший Эйнштейну создавать математический аппарат теории относительности. Он в 1908 г. и объединил пространство и время в единое четырехмерное пространство-время.
Поскольку движения во времени из прошлого в будущее мы не видим, а только понимаем (мним), что оно существует, Минковской назвал четвертую (временную) ось координат мнимой.
Если трехмерное пространство еще можно изобразить на листе бумаги с помощью изометрии, то четырехмерное уже невозможно. Но СТО первоначально рассматривала только прямолинейные и равномерные движения тел вдоль одной оси координат. Поэтому Минковский вслед за составителями графиков движения поездов стал откладывать на одной оси координат плоскости листа бумаги расстояния l в трехмерном пространстве, а на другой, перпендикулярной ей оси - мнимые "расстояния" во времени iСt Здесь символ означает мнимую единицу, а на скорость света в вакууме С домножено для того, чтобы "расстояния во времени" имели ту же размерность (метры), что и расстояния в пространстве.
В результате получилась комплексная плоскость (l,iСt ), действительная и мнимая оси координат которой пересекаются в точке 0, принятой за начало отсчета координат. Всякая точка на такой плоскости в математике описывается комплексным числом

(1.1)

Теория комплексных чисел к началу XX века была уже достаточно хорошо разработана математиками. Поэтому далее разработчикам СТО требовалось лишь строго следовать ей. Но они этого не сделали, а начали изобретать свою смесь теории комплексных чисел с векторной алгеброй.
В последней длинавектора, илиотрезка ∆l, связанас длинамиего проекций (∆х, ∆у, ∆z) надекартовы осикоординат теоремой Пифагора:

(1.2)

Минковский стал вычислять расстояние ∆l между точкамичетырехмерного пространства-временипо тому же правилу:

(1.3)

А поскольку то данное выражение он переписал в виде:

(1.4)

Появившийся здесь знак минуса противоречил теореме Пифагора, требовавшей плюса. Тогда создатели СТО и сформулировали "псевдопифагорову теорему": квадрат гипотенузы равен разности квадратов катетов И хотя треугольника такими свойствами не начертить даже с помощью неэвклидовой геометрии Римана, ссылки на которую любил делать Эйнштейн, объяснили, что такова уж особенность четырехмерного пространства-времени. Эйнштейн назвал это эфемерное пространство "квазиэвклидовым" [10].
Для чего потребовалась столь смелая "модернизация" геометрии? Дело в том, что в классической механике преобразования Галилея при переходе от одной инерциальной системы отсчета координат к другой оставляли неизменным расстояния в трехмерном пространстве. Разработчикам СТО хотелось, чтобы по аналогии с этим используемые ими преобразования Лоренца, заменившие в СТС преобразования Галилея, оставляли неизменной (инвариантной) не только скорости света С (для чего они и были найдены X. Лоренцем), но и расстояние между точкам! четырехмерного пространства - времени [11]. Однако величина ∆К, вычисляемся и; формулы (1.3) оставалась инвариантной при преобразованиях Лоренца только когд; в формуле (1.4) между ее слагаемыми был знак минуса. Более того, когда и само значение брали со знаком минуса. В конце концов разработчики СТО записали:

(1.5)

Определяемую так величину ∆S назвали интервалом, понимая его какрасстояы между точками пространства-времени [12].
Казалось бы, что все вроде правильно, хотя и требовало ломки сложившихся представлений эвклидовой геометрии, принятия без доказательств "псевдопифагоровой теоремы" и отказа даже от попыток наглядно представить происходящее в "псевдоэвклидовом" пространстве. Но этот отрыв физики от наглядности скоро был объяв лен не недостатком, а достижением теории.
Благодаря своей инвариантности, облегчающей расчеты, понятие интервала как расстояния между точками "четырехмерного континуума" стало широко использоваться в СТО, а затем и в ОТО, где все зиждется на понятии об интервале. Но разберемся, насколько верно его определение.
Точку в четырехмерном пространстве-времени Минковского, называемом "миром Минковского", описываемую комплексным числом (1.1), в СТО называют "мировой точкой". При ее движении в пространстве - времени она рисует на плоскости листа бумаги "мировую линию".
Комплексная длина бесконечно малого отрезка этой линии, или дифференциал комплексного числа, в теории комплексных чисел определяется выражением [13]:

(1.6)

Возведем этот дифференциал во вторую степень:

(1.7)

Мы получили новое комплексное число. В нем выражение в квадоатных скобках, являющееся действительной его частью, и есть та самая величина которую мы видели в формуле (1.4). Поэтому можно сделать вывод, что то выражение, которое в СЮ называют квадратом дифференциала интервала dS и понимают его как квадрат бесконечно малого расстояния между точками пространства-времени, на самом деле является лишь взятой с противоположным знаком действительной частью квадрата бесконечно малого отрезка комплексной длины мировой линии.
А вот мнимая его часть ускользнула от внимания разработчиков СТО. И только в ОТО мнимая часть выражения (1.7) была учтена, хотя разработчики ОТО так и не осознали, что интервал - это отнюдь не расстояние между точками пространства-времени. Но не будем углубляться в ОТО, а вернемся к комплексной плоскости мира Минковского, точку на которой описывает комплексное число (1.1).
В теории комплексных чисел расстояние между точками комплексной плоскости вычисляют как модуль (абсолютную величину) разности комплексных чисел, описывающих данные точки. Этот модуль определяют из теоремы Пифагора:

(1.8)

Видим, что ошибка Минковского состояла в том, что он напрасно оставлял в выражении (1.3) символ i, а затем возводил его во вторую степень и совершенно напрасно поставил в получившемся выражении (1.4) знак минуса.
Чем же тогда на самом деле является так называемый интервал ∆S, определяемый из выражения (1.5), если это не расстояние между точками пространства-времени?
Чтобы ответить на этот вопрос, надо, оказывается, сначала внимательно разобраться в том, как определять скорость движения в пространстве-времени. В классической механике среднюю скорость V движения тела в пространстве определяют как отношение длины пути пройденного телом, ко времени ∆t, за которое пройден этот путь. А мгновенную скорость V определяют как производную от l по dt (11. Если по аналогии с этим определять скорость движения точки в пространстве - времени "мира Минковского", то надо взять производную по dt от комплексного числа К, описывающего данную точку:

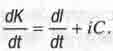(1.9)

Действительная часть здесь оказалась не чем иным, как скоростью V движения точки в пространстве, определяемой классической механикой. Это должно бы Радовать, так как соответствует принципу дополнительности. Однако мнимая временная) часть у получившегося выражения (1.9) оказалась константой С. Из этого можно было бы сделать ошибочный вывод, что всякое тело всегда движется во времени с постоянной скоростью С, которая ни от чего не зависит. Но это противоречило бы! самой же теории относительности, открывшей людям, что ход времени на движущемся теле зависит от скорости его движения в пространстве. (Несложно понять, что ход времени и скорость движения во времени - величины взаимосвязанные).
Г. Минковский нашел выход (к сожалению, как мы сейчас покажем, не наилучший) из этого затруднительного положения - стал определять скорость движения точки в пространстве-времени как производную от К по собственному времени , отсчитываемому часами, перемещающимися вместе с движущимся телом! (измеряемому его собственными часами).
Ведь Эйнштейн уже в первой своей публикации [1] 1905 г. по СТО показал, чтя движущиеся часы должны идти медленнее неподвижных, и что при движении тела ‹ t в соответствии с его формулой

(1.10)

Поэтому при дифференцировании комплексного числа (1.1) по мнимая часта получающегося выражения уже не была константой. Определяемую так скорость; движения точки в пространстве-времени своего "мира" Минковский назвал "четырехскоростью":

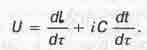(1.11)

Он отмечал, что достоинством такого определения является то, что дифференцирование осуществляется по величине d , которая инвариантна при преобразованиях Лоренца, что облегчало расчеты.
Физики и по сей день пользуются таким определением четырехскорости, записывая его, правда, в несколько ином виде:

(1.12)

который делает четьюехскорость безразмерной величиной (здесь j=1, 2, 3, 4;
Но обратим внимание на то, что мнимая (временная) часть четырехскорости в выражении (1.11) при V > О больше скорости света С и устремляется к бесконечности, когда V —›С. Да и действительная часть четырехскорости
возрастая с ростом скорости V, становится больше скорости света С, когда V превышает величину Это как-то не очень вяжется с постулатом Эйнштейна, провозглашающим, что в природе не существует скоростей движений тел, больших скорости света в вакууме С. Разработчикам СТО не удалось найти выхода из этой щекотливой ситуации, и тогда четырехскорость (1.11) и была преобразована в безразмерную величину (1.12) чтобы хоть как-то завуалировать указанное противоречие.
А ведь оно возникает лишь от того, что величины l и взяты из разных систем отсчета: l - из неподвижной, связанной с наблюдателем, относительно которого происходит движение, - из движущейся, связанной с перемещающимся телом. Так определять скорость движения тела некорректно!

1.3. Новое определение скорости движения во времени и основное уравнение теории движения

В книге [8] впервые дано новое определение мнимой скорости движения тела во времени, позволяющее освободить теорию относительности от указанных выше недочетов, которые более 80-ти лет сдерживали ее развитие. По аналогии с вышеприведенным классическим определением скорости V движения тела в пространстве, в [8] скорость у мнимого движения тела во времени выражается в секундах "пути" во времени, проходимого телом за время t, отсчитанное часами наблюдателя, относительно которого движется данное тело. В результате получается безразмерная величина

(1.13)

Понятно, что мгновенное значение скорости движения во времени определяется дифференциалами:

(1.14)

покоящегося в пространстве тела = t, поэтому А с увеличением скорости V движения тела величина становится меньше, чем t, как это следует из эйнштейновской формулы (1.10) и из многочисленных результатов экспериментов по измерению времени "жизни" ускоренных элементарных частиц, проводившихся в разных странах с 40-х годов. Поэтому безразмерная скорость у движения тела во времени уменьшается с ростом скорости V движения его в пространстве, становясь меньше единицы при
Кстати, скорость движения тела в пространстве тоже можно преобразовать в безразмерную, если разделить V на С. Безразмерная скорость движения тела в пространстве

(1.15)

(физики называют эту величину "релятивистским фактором") тоже не может превышать единицу, поскольку У не может превысить скорость света.
Анализ многочисленных экспериментов по измерению времени "жизни" неустойчивых к распаду элементарных частиц, ускоренных до самых разных скоростей V, проводившихся с 40-х годов, показывает, что во всех случаях соблюдается уравнение

(1.16)

Это основное уравнение теории движения, предложенной в [8, 9] вместо СТО. Здесь оно приведено как эмпирическое, но к нему можно прийти и логическим путем, "сходя из того, что каждая из взаимосвязанных величин ß и y не может превышать единицу. Но еще проще уравнение (1.16) получить простым алгебраическим преобразованием эйнштейновской формулы (1.10).
Из нее понятно, что этот радикал, фигурирующий в большинстве формул и уравнений СТО , долгие годы называли "фактором Лоренца", не догадываясь, го это еще и безразмерная скорость движения тела во времени.
В книге [8] величины , являющиеся решениями уравнения (1.16), рассматриваются как действительная и мнимая части комплексной скорости движения тела

(1.17)

Ее модуль, согласно (1.16), всегда равен единице (или |С|, если мы почленно домножим обе части уравнения (1.17) на С, чтобы превратить безразмерные скорости в имеющие размерность м/с). Это значит, что абсолютная величина комплексной скорости движения любого тела всегда равна скорости света в вакууме С.

1.4. Что такое интервал и новое определение осей координат четырехмерного пространства-времени, возвращающее его к эвклидовой геометрии

Вернемся к вопросу о том, что такое интервал. Приняв новое определение "пути во времени" т, мы должны заменить на комплексной плоскости "мира Минковского" ось OlCt осью OlC. Всякая точка на такой новой комплексной плоскости теперь будет описываться комплексным числом

(1.18)

Его можно получить и другим путем: домножив на С обе части выражения (1.17) и проинтегрировав их по dt.
Непривычной и необычной, на первый взгляд, получается наша новая комплексная плоскость, одна координата (l) на которой определяется измерениями одного наблюдателя, а другая (Сг) - другого, движущегося относительно первого. Но ведь это комплексная плоскость расстояний. Ее ось Ol - это ось расстояний в пространстве, которые проходит тело за время t, отсчитываемое часами неподвижного наблюдателя, другая же ее ось OiC - это ось "расстояний" С во времени, которые проходит то же тело за то же время t, отсчитываемое часами того же наблюдателя, относительно которого движется данное тело.
Определим теперь квадрат расстояния между точками 0 и Z нашей комплексной плоскости (l, iC) как квадрат модуля комплексного числа

(1.19)

Если подставить сюда значения l = ßCt и - уt, то с учетом уравнения (1.16) получим:

(1.20)

Это значит, что расстояние от начала осей координат до точки Z нашего четырехмерного "мира" равно Сt. Полученный результат отражает тот уже отмечавшийся выше факт, что все тела в нашем комплексном ространстве-времени движутся с одной и той же по абсолютной величине комплексной скоростью J, имеющей модуль |С|.
А вот если подставить полученное значение вместо в (1.19), будем иметь:

(1.21)

Левая часть этого уравнения есть не что иное, как известное и бывшее столь загадочным выражение (1.5) для квадрата интервала. Значит, интервал 5 - это "расстояние" Ст, которое проходит тело во времени за время t, выраженное благодаря коэффициенту С в тех же единицах длины (метрах), что и расстояние I, проходимое этим телом в пространстве за то же время т., отсчитанное наблюдателем, относительно которого движется данное тело.
Впрочем, формулу dS = Cd нам и доказывать не надо, она давно известна в СТО [14].
С учетом этого запишем окончательное выражение для квадрата расстояния ∆ между точками нашего комплексного пространства-времени:

(1.22)

Как видите, это расстояние определяется теоремой Пифагора. А еще видим, что это фактически то же самое выражение, что и эйнштейновское (1.5) для квадрата интервала. Только теперь оно записано в нормальном виде: квадрат гипотенузы С∆t равен сумме квадратов катетов
Эвклидова геометрия восторжествовала! И уже не нужны ни "псевдопифагорова теорема", ни "квазиэвклидовое пространство", бывшие, как мы теперь понимаем, вынужденными уловками разработчиков СТО на неосознанном ими пути к уравнению (1.22), задаваемому самой Природой.

1.5. Основная диаграмма теории движения

Основное уравнение (1.16) теории движения является не чем иным, как каноническим уравнением плоской центральной кривой второго порядка

Его решения - попарные значения величин ß и у, удовлетворяющие этому уравнению. Совокупность всех возможных решений образует на комплексной плоскости (ß,iу) график уравнения (1.16).
Если ß и у - действительные числа, то графиком уравнения (1.16) является окружность, имеющая радиус, равный единице (см. рис. 1.1). Эту окружность описывает вокруг начала осей координат на комплексной плоскости конец радиуса-вектора комплексной скорости

Взаимно перпендикулярными осями координат этой плоскости является действительная ось Oß безразмерной скорости движения материальной точки в пространстве (ось абсцисс) и мнимая ось Оiy безразмерной скорости движения той же точки во времени (ось ординат). Длина радиуса - вектора J, принятая за единицу, равна модулю комплексного числа J, характеризующего движение этой материальной точки в комплексном пространстве - времени нашего четырехмерного мира. Вся теория движения, изложенная выше, а подробнее в [8], вытекает из графика этой окружности.

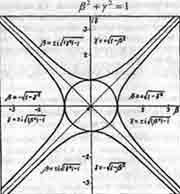
Рис. 1.1. Основная диаграмма теории движения (9).

Но до сих пор мы рассматривали только действительные значения величин ß и у А ведь существуют и мнимые числа, которые в математике имеют не меньшие права, чем действительные. Предположим, что безразмерная скорость ß движения объекта в пространстве выражается положительным или отрицательным мнимым числом. Тогда уравнение (1.16) останется справедливым, если скорость движения того же объекта во времени

(1.23)

по абсолютной величине будет больше единицы. Притом величины у будут оставаться действительными числами, принимающими положительные и отрицательные значения.
Основное уравнение (1.16) при и при ß -мнимом превращается в уравнение гиперболы:

(1.24)

Верхняя и нижняя ветви этой гиперболы (см. рис. 1.1) касаются единичной окружности в точках пересечения с осью ординат.
Отметим, что абсолютные величины удовлетворяющие уравнению (1.24), не имеют ограничений сверху. То есть они лежат в пределах

(1.25)

Отметим еще, что при мнимом ß комплексная скорость становится чисто мнимой величиной.
Как видим, скорости движения ß по своей абсолютной величине здесь могут называться за пределами дозволенного теорией относительности, то есть становятся больше единицы, а скорости у вообще всегда больше единицы, если ß - мнимое число. Поэтому области на рис. 1.1, описываемые верхней и нижней ветвями гиперболы (1.24), названы в книге [9] "вертикальным запредельным миром", в отличие от допредельного мира, описываемого единичной окружностью, характеризующей поступательное движение обычных тел с досветовыми скоростями.
Предположим теперь, что мнимым числом является величина безразмерной скорости у движения объекта во времени. Тогда основное уравнение (1.16) останется справедливым, если величина безразмерной скорости движения этого объекта в пространстве

(1.26)

по абсолютной величине будет больше единицы. Притом (3 будет оставаться действительным числом (положительным или отрицательным). Основное уравнение (1.16) при |ß|>= 1 и при мнимых превращается в уравнение гиперболы, сопряженной с предыдущей:

(1.27)

Правая и левая ветви этой гиперболы (см. рис. 1.1) касаются единичной окружности в точках пересечения с осью абсцисс.
И опять абсолютные величины безразмерных скоростей ß и у не имеют ограничений сверху:

(1.28)

А комплексная скорость движения J=ß + iy становится чисто действительной величиной (так как мнимая ее часть iy=i(|iy|)=-|y| становится действительным числом).
Области на рис. 1.1, описываемые правой и левой ветвями гиперболы (1.27), названы в книге [9] "горизонтальным запредельным миром". В этом мире должно наблюдаться довольно странное явление. А именно, в результате того, что мнимая часть комплексной скорости J становится действительным числом, движение во времени тут становится реальным, а не мнимым! Это означает, что объект, совершающий такое движение, не может быть обнаружен ни в какой точке времени, так как непрерывно перемещается сквозь "пласты времени", как бы пересекая их. Если в данный момент (по нашим часам) он в течение какого-то мгновения, продолжительность которого определяется, по-видимому, соотношением неопределенностей квантовой механики, присутствует в нашем мире вместе с нами, то в следующий миг он уже во вчерашнем или в завтрашнем нашем дне, в то время как мы остались в сегодняшнем и медленно движемся в завтрашний вместе с окружающими нас реальными предметами нашего мира досветовых скоростей. В результате этот объект, который можно назвать виртуальным, сегодня для нас уже недосягаем и неуловим. В книге [9] показано, что правая и левая полуветви основной диаграммы теории движения описывают движение гипотетических сверхсветовых частиц - тахионов, теорию которых физики начали разрабатывать еще в 60-е годы [15]. Но экспериментаторам несмотря на многочисленные попытки, до сих пор не удалось зарегистрировать тахионы, по-видимому в силу вышеуказанной их особенности движения во времени, делающей тахионы почти ненаблюдаемыми.
Понимание этой особенности, дающееся теорией движения, может теперь позволить экспериментаторам по-иному взглянуть на проблемы регистрации тахионо Более того, теория движения, дающая новый мощный толчок развитию теории там онов, указывает, что виртуальные частицы в квантовой теории поля - это тахиож что неуловимые гравитоны - это тоже тахионы, а потому гравитация распространяв ся со скоростями, на много порядков величины превосходящими скорость света вакууме. Более того, в книге [9] показано, что всепроникающие нейтрино - это, по видимому, тоже тахионы! А нейтрино уже зарегистрированы экспериментально. Значит, тахионы все-таки можно регистрировать?
Теория движения показывает, что виртуальный мир сверхсветовых частиц должен быть столь же богат (если не богаче), как и наш мир досветовых частиц. Богаче с может быть хотя бы потому, что тахионы обладают способностью двигаться во врем< ни как вперед, так и назад (а мы - только вперед). В [9] развивается гипотеза укр< инского физика из г. Бердянска М. Т. Попова о том, что именно тахионы нес] информацию из будущего, которую каким-то образом воспринимают ясновидцы гадалки.
В заключение данной главы отметим следующее. Если движение объектов в "горизонтальном запредельном мире" описывается чисто действительной скоростью, а движение объектов "вертикального запредельного мира" - чисто мнимой J, то читатели могут подумать, что объекты "вертикального запредельного мира" обнаружить еще сложнее, чем "горизонтального". Но четвертая глава покажет, что наоборот. Более того, читатели увидят, что с объектами "вертикального запредельного мирг они имеют дело буквально на каждом шагу и хорошо с ними знакомы. Только вс достаточно ли хорошо?

Выводы к главе

1. В матаматическом аппарате СТО, пренебрегший привилами теории комплексных чисел, допущен ряд ошибок. Самая важная из них - неправильное понимание интервала как расстояния - "путь", проходимый телом в собственном времени за время движения этого тела в пространстве, выраженный в единицах длины.
2. Скорость движения тела во времени следует определять подпбно скорости движения его в пространстве как производную от пути по времени t, измеряемому наблюдателем, относительно которого движется данное тело.
3. точку пространства - времени следует описывать не комлексным числом , как это делал Г. Минковский, а комплексным числом . Это значит, что четвертой осью координат пространства - времени является ось , а не ось .
4. Безразмерная скорость движения тела во времени y и безразмерная скорость движения его в пространстве (где С - скорость света в вакуума) связаны основным уравнением теории движения .
5. Кроме действительных решений (попарных чискел ), графиком которых является единичная окружность, основное уравнение теории движения имеет еще два семейства мнимых решений, гкафиками которых являются гиперболы. При мнимых y основное уравнение описывает движение частиц со сверсветовыми скоростями (тахионов), а при мнимых ß - вращательное движение тела, имеющего в результате вращения скорость движения во времени y больше единици.

Содержание